Rekurencja (rekursja)

Rekurencja znana też jako rekursja to termin związany zarówno z matematyką jak i informatyką i w obu przypadkach ma podobne znaczenie - najłatwiej jest ją właśnie wytłumaczyć na najbardziej popularnych funkcjach matematycznych. W lekcji tej omówię:

Co to jest rekurencja

Rekurencja jest to sytuacja, w której funkcja (czy też w naszym przypadku metoda) wywołuje samą siebie w celu rozwiązania pewnego problemu - stąd m.in. słynne już powiedzenie żeby zrozumieć rekurencję, trzeba zrozumieć rekurencję. W wielu sytuacjach pozwala w znaczny sposób uprościć zapis iteracyjnego rozwiązania naszego problemu (na przykład skomplikowanej pętli) - jednak jak się później dowiesz, nie zawsze jest to dobry pomysł. W tym momencie może Ci się także wydawać, że metoda wywołując samą siebie doprowadzi do sytuacji typu nieskończona pętla - i tak może się zdarzyć, jednak dzięki odpowiedniemu zapisowi można się przed tym zabezpieczyć.

Zastosowanie

Rekurencja wykorzystywana jest w wielu sytuacjach, jednak najpopularniejsze to:

• algorytmy wyszukiwania (na przykład quick sort)

• rekurencyjne struktury danych (na przykład lista wiązana)

• specyficzne algorytmy, w których wykorzystanie rekurencji jest czymś naturalnym

To co ciekawe to fakt, że każde rozwiązanie rekurencyjne można odwzorować w formie klasycznej - iteracyjnej. Jak się jednak z pewnością nie raz przekonacie jest to często problem skomplikowany nie tylko pod względem programistycznym, ale także matematycznym. Gdybyśmy narysowali wywołania rekurencyjne na kartce to najprawdopodobniej przybrałyby one postać albo jednej długiej linii z kolejnymi wywołaniami metod, albo strukturę drzewiastą - co jest przyczyną późniejszych problemów, bo na stosie wywołań zaczyna brakować w takiej sytuacji miejsca.

Przykłady

W przykładach pokażę różne metody w dwóch wersjach - tradycyjnej i rekurencyjnej. Mam nadzieję, że dzięki temu każdy zobaczy na czym polega różnica i jak rekurencja może ułatwić nam życie.

Przykład 1 - Sumowanie

Metoda, która sumuje wszystkie liczby naturalne mniejsze, lub równe liczbie podanej jako parametr.

public class Rekurencja {
 
 	public int sumaIteracja(int n) {
 		int suma = 0;
 		while(n > 0) {
 			suma = suma+n;
 			n--;
 		}
 		return suma;
 	}
 
 	public int sumaRekurencja(int n) {
 		if(n>0) {
 			return n + sumaRekurencja(n-1);
 		} else {
 			return 0;
 		}
 	}
 
 	public static void main(String[] args) {
 		Rekurencja r = new Rekurencja();
 		int iteracja, rekurencja = 0;
 
 		iteracja = r.sumaIteracja(3);
 		rekurencja = r.sumaRekurencja(3);
 
 		System.out.println("Iteracja: "+iteracja);
 		System.out.println("Rekurencja: "+rekurencja);
 	}
 }

Jak widać w obu przypadkach otrzymujemy dokładnie taki sam wynik, czyli 6. Zobaczmy jednak jak to działa. W przypadku wersji iteracyjnej nie ma większego problemu - przekazujemy jako parametr liczę ograniczającą nas z góry i dodajemy od końca (można zrobić dodawanie od 1 - nie ma to znaczenia). Na końcu zwracamy sumę - dodatkową zmienną, w której przechowujemy wszystkie dodane składniki.

W przypadku wersji rekurencyjnej dzieje się jednak coś dziwnego - sprawdzamy, czy parametr jest większy od 0, jeśli tak to zwracamy sumę tej liczby i wraz z wywołaniem funkcji z parametrem o 1 mniejszym, jeśli parametr jest mniejszy, lub równy 0 t zwracamy 0. Dziwne prawda? Najłatwiej pokazać jak to działa w Excelu za pomocą prostej hierarchii.

Ważne tutaj jest to, że wywołanie np. sumaRekurencja(2) nie ma pojęcia o tym, że jest składnikiem sumy w sumaRekurencja(3) - elementy są odkładane na stosie, a następnie zbierane od końca - tak naprawdę nie dodajemy 3+2+1+0, tylko 0+1+2+3.

Jako ciekawostkę warto wiedzieć, że można tutaj wykorzystać również operator trójargumentowy (ternary operator) zapisując ciało metody sumaRekurencja() w jednej linijce:

public int sumaRekurencja(int n) {
 	return n>0? n+sumaRekurencja(n-1) : 0;
 }

Prawda, że fajne? Warto o tym pamiętać - to zazwyczaj +10 do szpanu na kursach z programowania na uczelni ;)

sumaRekurencja(3);

3 + sumaRekurencja(2);

sumaRekurencja(2);

3 + 2 + sumaRekurencja(1);

sumaRekurencja(1);

3 + 2 + 1 + sumaRekurencja(0);

sumaRekurencja(0);

3 + 2 + 1 + 0

sumaRekurencja(1);

3 + 2 + 1

sumaRekurencja(2);

3 + 3

sumaRekurencja(3);

return 6

Przykład 2 - Ciąg Fibonacciego

Ciąg Fibonacciego - działa również dla liczb naturalnych. Jeśli liczba jest mniejsza od 2 zwracamy tę liczbę, dla liczb większych od 2 zwracamy sumę składającą się z wyniku wywołania tej samej funkcji dla parametru pomniejszonego o 1, oraz pomniejszonego o 2. Zapisać można to w postaci:

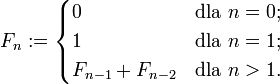
Wydaje się proste - i faktycznie takie jest, jednak nie do końca - istnieje spór co do tego, czy element 0 powinien być wliczany jako element ciągu - my go potraktujemy jako element 0, czyli nie będziemy go uwzględniali w naszych metodach - wywołując metodę z parametrem 5 otrzymamy wynik dla 5 elementu Fibonacciego licząc od 1 (czyli otrzymamy wartość 5). Więcej informacji na temat tego ciekawego ciągu znajdziecie na wikipedii.

Zapiszmy więc ponownie dwie wersje.

public class Fibonacci {
 
 	public int fibonacciIteracja(int n) {
 		int pierwszy = 1;
 		int drugi = 1;
 		int pomocnicza = 1;
 
 		for(int i=2; i<n; i++) {
 			pomocnicza = pierwszy + drugi;
 			pierwszy = drugi;
 			drugi = pomocnicza;
 		}
 
 		return pomocnicza;
 	}
 
 	public int fibonacciRekurencja(int n) {
 		return n<2? n : fibonacciRekurencja(n - 1) + fibonacciRekurencja(n - 2);
 	}
 
 	public static void main(String[] args) {
 		Fibonacci fibo = new Fibonacci();
 		int fiboIter, fiboRek = 0;
 
 		fiboIter = fibo.fibonacciIteracja(6);
 		fiboRek = fibo.fibonacciRekurencja(6);
 
 		System.out.println("Iteracja: "+fiboIter);
 		System.out.println("Rekurencja: "+fiboRek);
 	}
 }

Jak widać w tym przypadku rozwiązanie rekurencyjne jest dużo bardziej intuicyjne - choć może wynik nie jest tak prosty do przewidzenia. W przypadku wersji iteracyjnej trzeba wprowadzić dodatkową zmienną, która będzie sumowała kolejne czynniki - te z kolei trzeba odpowiednio podmieniać przy kolejnych przejściach pętli. Widać dodatkowo jak można skrócić kod wykorzystując zapis rekurencyjny.

Ciąg fibonacciego różni się od sumowania z Przykładu 1 tym, że wywołania rekurencyjne zaczynają tutaj tworzyć wraz z kolejnym poziomem drzewo - każde wywołanie funkcji dla wartości wyższych od 2 powoduje wywołanie funkcji kolejne 2 razy.

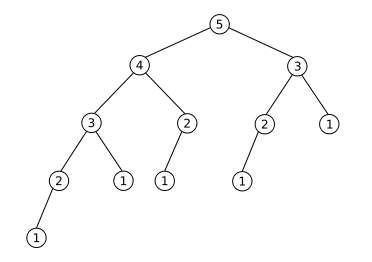
Można więc sobie wyobrazić jak zaczyna wyglądać stos dla wywołania rekurencyjnej funkcji fibonacciego z argumentem typu 100 - w Excelu nie ma nawet sensu tego rozpisywać.

Problemy

Najwięcej problemów związanych z rekurencją wiąże się z ograniczeniami stosu wywołań, a właściwie jego pojemności. Na stosie tak jak wcześniej pokazaliśmy są odkładane kolejne wywołania danej metody i dopiero gdy dojdziemy do ostatniego elementu dane te są zbierane - bardzo łatwo więc o sytuację, gdy po prostu stos przepełnimy. Żeby zobaczyć co się w takiej sytuacji dzieje, spróbujcie uruchomić pierwszy z powyższych przykładów z wartością typu 10000. Jak widać otrzymujemy błąd StackOverflowError. Można sobie z tym poradzić na dwa sposoby:

• zwiększyć rozmiar stosu - co oczywiście jest najgorszym co możemy zrobić i powinna to być ostateczność

• optymalizacja i przerobienie metody na rekurencję ogonową - kolejne wywołanie metody otrzymuje jako drugi parametr aktualną wyliczoną wartość, dzięki czemu na stosie nie są odkładane kolejne elementy (niestety Java nie wspiera rekurencji ogonowej),

• przepisanie algorytmu w wersji iteracyjnej.

Drugi problem to czas wykonania - spróbujcie wywołać drugi przykład (wersję rekurencyjną i iteracyjną osobno, wykomentujcie odpowiednie linijki kodu) z wartością typu 100. Pomijając tutaj problem z wykroczeniem wartości poza zakres int'a widać, że na obliczenie wartości za pomocą funkcji rekurencyjnej można czekać i czekać ... Widać tutaj zdecydowaną przewagę rozwiązania iteracyjnego.

Kiedy zatem stosować rekurencję?

Przede wszystkim w oczywistych jej zastosowaniach, gdy mamy pewność, że nie spowoduje ona dużego spadku wydajności naszej aplikacji. Funkcję należy przede wszystkim przetestować dla wartości granicznych - jak widać na naszym przykładach to, że coś działa dla argumentu 5, nie oznacza, że będzie działać równie dobrze dla wartości 100.